
電磁気学が苦手なのに電気系大学に進学してしまった元大学生です
四端子回路についてこれから学ぶor授業受けたけど分からなかったという未来の後輩たちのために、今回は備忘として自分なりに理解したことを記事として書きます。
これは、私と同じように「答えを見てもいきなり式がでてきて『!?』ってなってる」「ネットで解き方漁ったけど小難しくてサッパリ」みたいな人向けの記事になります。
目次
四端子回路(二端子対回路)のどこに躓いているか把握しましょう
解けるようになってから私がつまずいていたのは四端子回路ではなくそれ以前の回路の解き方だったことに気が付きました。
わたしの場合は、開放した時の電圧がどうなるのか…というそもそもの理論がよく分からなくてつまづいていました。皆さんはどうでしょうか?
この単元でつまづきやすい人はこんな人たちです。
- 線形代数がよく分からない
- 回路がつながっていないときの電圧の計算がよく分からない
実は四端子回路はそんなに難しいことをしていないです。
なので「わけが分からないよ」という人はそれ以前の回路の計算を立てる箇所で躓いている可能性が高そうです。
とりあえず急いでいる人は何をしたらいいのか
まず四端子回路ですが、基本と言える問題はそんなに多くないです。
π型、T型、あとは抵抗が1~2個含まれた回路の答えが出せるならあとは掛け合わせで何とかなります。
明日追試!などとにかく急いでいる方はとりあえず使われている式の丸暗記から始めるのが楽かと思います。
答え丸暗記→逆算できるようになればなんとなく知識もついてきます。
とりあえず、F行列でもZ行列でもY行列でも試験に関わるものは覚えてしまいましょう。

丸暗記が難しいから苦労したんですけどね……。
あと四端子回路で検索しつくして分からなかった人は、二端子対回路の方でも検索してみてください。四端子回路も二端子対回路も同じ回路のことを指します。
全然違うサイトが検索できるので参考になるかもしれません。逆もまた然りです。
ここから先は私がつまずいた部分と自分なりの解説を載せておくので参考にしてもらえれば嬉しいです。
とりあえずF行列(四端子定数)についてまとめてみる

F行列とは
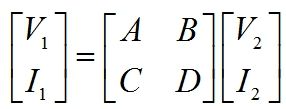
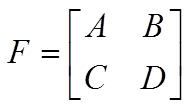
これのこと。
参考書などに普通に載ってると思います。
これについては本当に「こういうもの!」と思って丸暗記するしかありません。

教科書や参考書によってはI2の向きが逆向きで「-I2」となっているものもあります。
その場合は当サイトで紹介する演習問題の解答のB,Dの値にも「-1」を掛けてください。
ネットで他サイトを見るとI2で計算しているサイトが多そうなので最近の流行りはI2なのかなと思っていますが、古い教科書だとことごとく-I2でF行列が紹介されています。
その辺は教授の好みに応じて融通を利かせましょう。最終的に展開して具体的な値を入れると同じ数式にはなります。
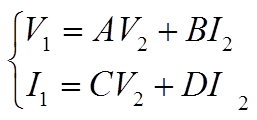
そして上の式を展開したのがコチラ。
展開方法を覚えてない人は行列を復習したほうがよさそうです。
これが求められると、四端子回路が複数連なっていた時にF行列を掛け合わせるだけで全体の電圧・電流が求められるので全部一気に計算するよりも簡単!というわけで重宝されている……らしいです。
具体的にどういう場合に使われているのかはお近くの教授までご質問をお願いします。
「Fパラメータを求めよ」「四端子定数を求めよ」と聞かれたときに求めたいのはこのABCDになります。
そして、ABCDを求めるにはどうすればいいのか。
I₂=0のとき、AとCが。V₂=0のとき、BとDが出てくる
I₂=0のときにAとC。V₂=0のときにBとDが求められることは、上式に実際に0を代入してみれば分かると思います。
そしてこの時の状態を
I₂=0のとき「2-2’が開放されている」 (つまり2-2’に何も繋いでない状態)
V₂=0のとき「2-2’が短絡されている」 (これは2-2’を銅線で繋いだ状態)
といいます。
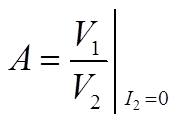
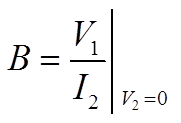
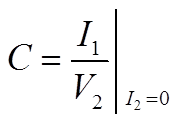
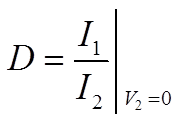
それぞれに0を代入して形を変えた式がこちら。
こんな感じで教科書で見るような形になります。
演習問題を解いてみる
まず抵抗1つの四端子回路を解いてみましょう。
テブナンの定理やキルヒホッフの法則を使えば普通に解けると思います。
演習その1
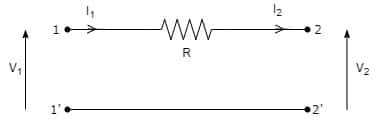
よく見る抵抗Rが横向きに1つついている回路になります。
この回路のFパラメータを求めてみましょう。
とりあえずA,Cを求めるために開放した時の回路を計算してみます。
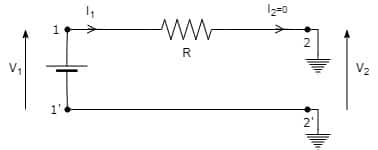
まず簡単なCから求めていきます。
見れば分かりますが、I2=0のときにI1=0となります。
断線している回路に電流は流れません。
C=I1/V2=0/V2=0となります。
つまり、C=0です。
次にAを求めていきます。
「見れば分かるよ!」という人も多いかと思いますが念のため。
V2=V1+I1*R
が今回求めたいV2部分の電位差になります。
Cの計算でI1=0であることは既に分かっているので、V2=V1となります。
要するにA=V1/V2=1となります。
次に閉塞回路でB,Dを求めていきます。
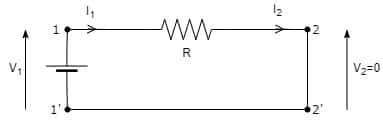
閉塞するとよく見る基本的な回路になるのでドツボにはまる人は少ないかなと思っています。
まずDの方が簡単なのでDから。
Rしかない回路であれば電流は並列でなければどこをとっても一定です。
つまりI1=I2となります。
D=I1/I2=1です。
最期にBを。
V1=RI1=RI2となります。
つまりB=V1/I2=Rです。
というわけでA=1、B=R、C=0、D=1が求められました!
演習その2
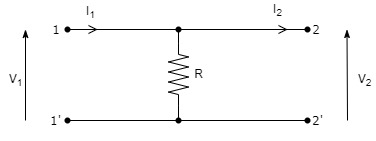
演習その1と同じように解いてみましょう。
まずは同じように開放状態の計算をしていきます。
もちろん、今回も同じようにI2=0のときにC=I1/V2となります。
開放状態のときV2=I1×Rなので、Cにそのまま代入するとC=1/Rとなります。
電圧は演習その1と同じようにV2=V1となります。電圧が減る要因である抵抗RがV2の中にしかないのでV1と同じ値なことは簡単にわかります。
A=V1/V2=1であることが分かりました!
次に閉塞状態ですね。
『2-2’をつないだ時は電流I1は邪魔者の抵抗Rのない2-2’の方へ全て流れる』というイメージを持つと(個人的には)計算しやすいです。
このイメージからD=I1/I2=1なのは割り出せるかなと思います。
最後にBですが、V1は(抵抗R前後の電圧の差+V2)になります。前提条件にあるとおり、閉塞状態なのでもちろんV2=0です。
そして抵抗Rの方向へは電流が流れていないので電圧の差も現れません。
なのでB=V1/I2=0ということがわかります。
というわけでA=1、B=0、C=1/R、D=1が求められました!
